PCA and Neural Network Autoencoder Connection#
We can learn principal component analysis (PCA) linear mapping from D-dimensions of data to M-dimensions of subspace where M < D by using a two-layer autoencoder neural network with linear activation. The model will learn to map from D-space to M-space by minimizing the mean squared error of the reconstruction and the true value.
The intuition why this is the case is because PCA is also a linear mapping that minimizes the mean squared error of the reconstruction of the datapoints from M-space to D-space.
In other words, PCA and a 2-layer neural network autoencoder are practically equivalent.
We load the Wine dataset from Sklearn which has 13 columns that are all float64 and 178 datapoints (rows)
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 13 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 alcohol 178 non-null float64
1 malic_acid 178 non-null float64
2 ash 178 non-null float64
3 alcalinity_of_ash 178 non-null float64
4 magnesium 178 non-null float64
5 total_phenols 178 non-null float64
6 flavanoids 178 non-null float64
7 nonflavanoid_phenols 178 non-null float64
8 proanthocyanins 178 non-null float64
9 color_intensity 178 non-null float64
10 hue 178 non-null float64
11 od280/od315_of_diluted_wines 178 non-null float64
12 proline 178 non-null float64
dtypes: float64(13)
memory usage: 18.2 KB
We show below a sample of the dataset
| alcohol | malic_acid | ash | alcalinity_of_ash | magnesium | total_phenols | flavanoids | nonflavanoid_phenols | proanthocyanins | color_intensity | hue | od280/od315_of_diluted_wines | proline | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 14.23 | 1.71 | 2.43 | 15.6 | 127.0 | 2.80 | 3.06 | 0.28 | 2.29 | 5.64 | 1.04 | 3.92 | 1065.0 |
| 1 | 13.20 | 1.78 | 2.14 | 11.2 | 100.0 | 2.65 | 2.76 | 0.26 | 1.28 | 4.38 | 1.05 | 3.40 | 1050.0 |
| 2 | 13.16 | 2.36 | 2.67 | 18.6 | 101.0 | 2.80 | 3.24 | 0.30 | 2.81 | 5.68 | 1.03 | 3.17 | 1185.0 |
| 3 | 14.37 | 1.95 | 2.50 | 16.8 | 113.0 | 3.85 | 3.49 | 0.24 | 2.18 | 7.80 | 0.86 | 3.45 | 1480.0 |
| 4 | 13.24 | 2.59 | 2.87 | 21.0 | 118.0 | 2.80 | 2.69 | 0.39 | 1.82 | 4.32 | 1.04 | 2.93 | 735.0 |
We then train a neural network autoencoder with linear activation functions that maps 13 input variables to 2 hidden nodes then back to 13 output nodes. The goal is to learn a 2D-mapping from 13D dataset such that we can linearly reconstruct from 2D to 13D with minimal mean squared error. We visualize the network architecture below.
Note that prior to training, we first standard scale the dataset so the values of the variables are comparable.
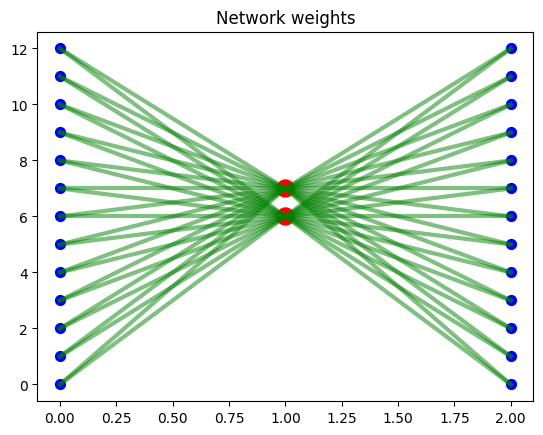
We visualize below the 2D space mapping of the datapoints, predicted vs true values correlation plot of the different variables pooled together, and the network weights over 200 training iterations. We see that the model learns to “spread” the data point projection in 2D space (chart 1).